Machine Learning 笔记（二）：单变量线性回归

线性回归 (Linear regression) 是一种以线性模型来建模自变量与因变量关系的方法。

分为：

• 单变量线性回归 (Linear regression with one variable)：只有一个自变量；
• 多变量线性回归 (Linear regression with multiple variable)：有多个自变量。

本篇先从单变量线性回归入手。

---

✎模型表达 (Model representation)

一个预测房价的例子：

给定某地不同面积房子的价格的数据集，希望通过该数据集构建一个模型，该模型能根据房子的面积来预测其价格。

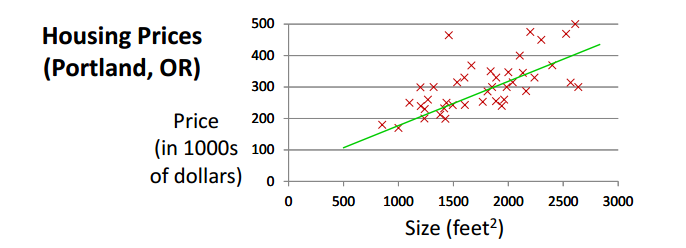
该例子属于 有监督学习 中的 回归 问题。

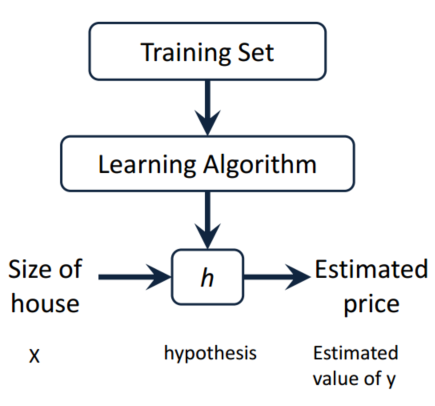
使用如下标记描述回归问题：

• m = Number of training examples （训练样例的数量）
• x’s = “input” variable / features （输入变量 / 特征）
• y’s = “output” variable / “target” variable （输出变量 / 目标变量）
• (x,y) - one training example （一个训练样例）
• (x⁽ⁱ⁾,y⁽ⁱ⁾) - ith training example （第 i 个训练样例）
• h (hypothesis) - h_θ(x) = θ₀+θ₁x （学习算法的解决方案或函数，将 x’s 映射到 y’s）

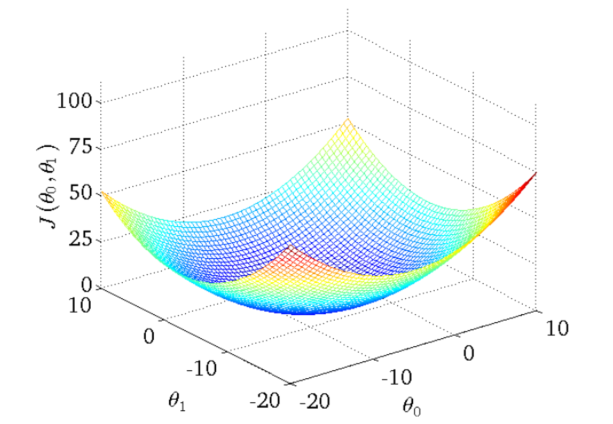
✎损失函数 (Cost function)

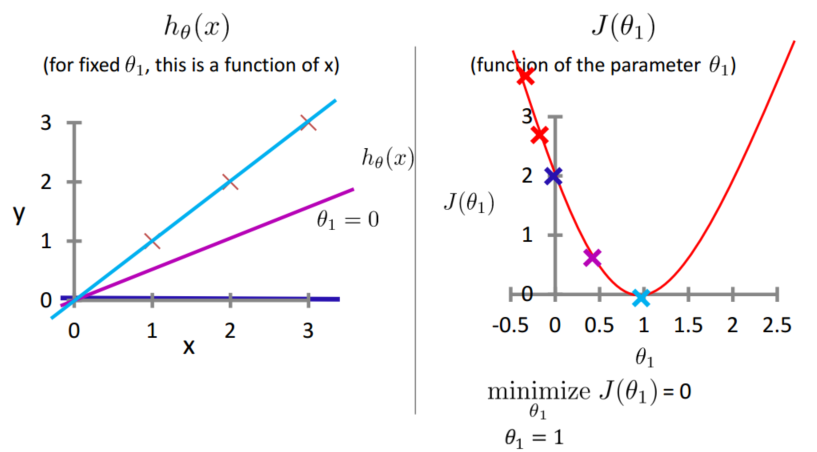
Hypothesis: h_θ(x) = θ₀+θ₁x , 参数 θ_i’s 如何选择？

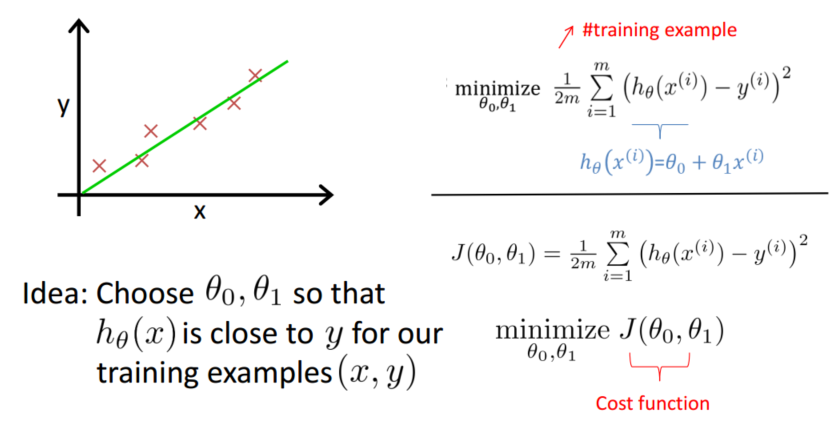
情形一：假定 θ₀ = 0，Cost function 变为 J(θ₁)

情形二：θ₀，θ₁ 都可变，Cost function 为 J(θ₀, θ₁)

✎