NLP 笔记（三）：最短编辑距离

发表于 | 更新于 | 分类于
本文字数： 1.6k | 阅读时长 ≈ 1 分钟

✎知识讲解

✎定义

如何衡量两个字符串有多相似？

  • 拼写纠正：用户键入“graffe”，以下哪个最接近？

    • graf
    • graft
    • grail
    • giraffe

  • 计算生物学：

编辑距离（Edit Distance）：两个字符串之间的最短编辑距离是指将一个字符串变换为另一个需要的编辑操作（插入(Insertion)，删除(Deletion)，替换(Substitution)）的最小数量。

例如：

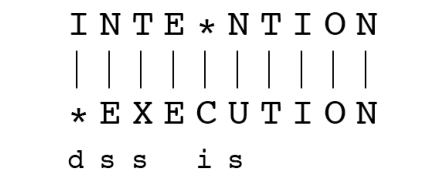
  • 如果每个操作的代价值为1，则此两个字符串之间的距离为5；
  • 如果替换操作的代价值为2，则距离为8。

如何得到最短编辑距离？

尝试：搜索从起始字符串到最终字符串的路径（编辑序列）：

  • 初始状态：需转换的词语
  • 操作：插入，删除，替换
  • 目标状态：需得到的词语
  • 路径代价：（即我们需尽量缩短的）编辑数量

这样，求最短编辑距离相当于搜索，但是所有编辑序列的空间很大，我们无法穷举！而且许多不同路径以相同的状态结束，因此无需跟踪所有这些路径，只需求出到最终状态的最短路径即可。

符号定义：对于两个字符串

  • X of length n
  • Y of length m

我们定义 D(i, j) 为 X[1...i]（X 的前 i 个字符）和 Y[1...j]（Y 的前 j 个字符）间的编辑距离。

因此 X 和 Y 间的编辑距离为 D(n, m)。

✎计算最短编辑距离

方法：动态规划（Dynamic Programming）

✎动态规划

  • 对 D(n, m) 的表格计算（tabular computation），通过把原问题分解为相对简单的子问题的方式来求解；
  • 特点：自底向上（Bottom-up）
    • 对于较小的 i, j 计算 D(i, j)
    • 对于较大的 i, j ，以之前的计算结果为基础得出 D(i, j)，0 < i < n，0 < j < m

✎算法实现

  • 初始化：D(i, 0) = i，D(0, j) = j

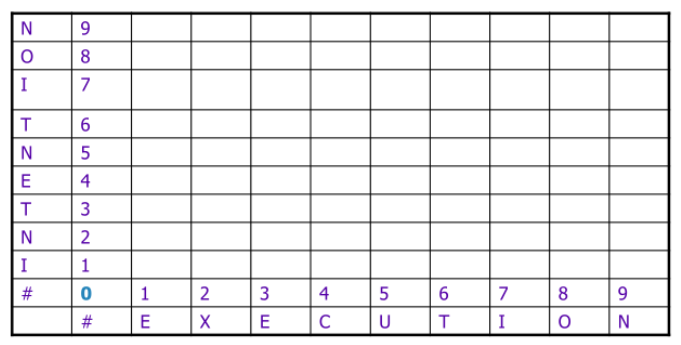
  • 递推关系：

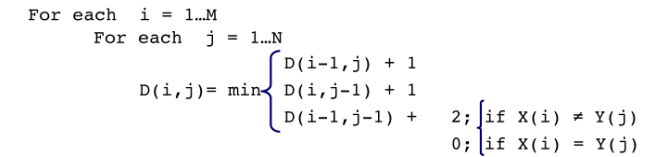
  • 终止：D(n, m) is distance

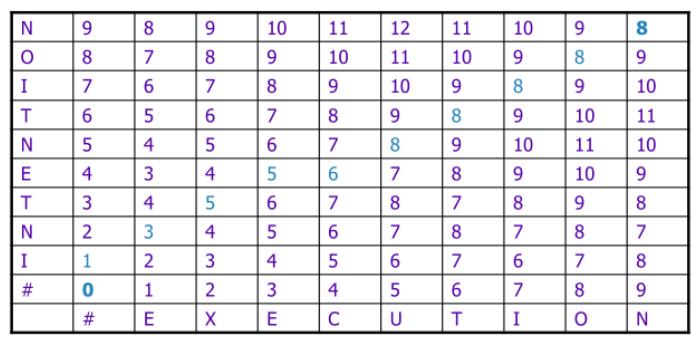
✎计算对齐的回溯

计算对齐（Computing alignments）：我们经常需要将两个字符串的每个字符彼此对齐，通过保持“回溯（backtrace）”来做到这点。

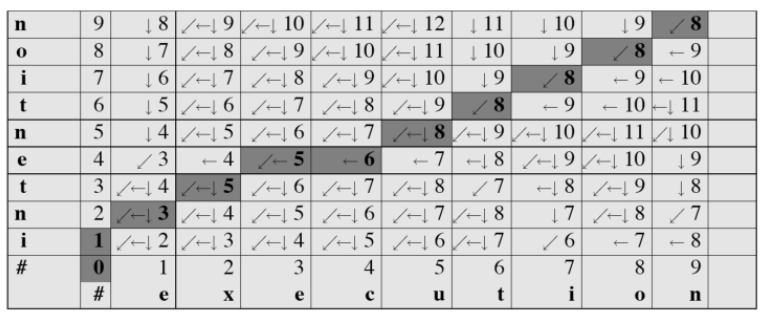
回溯得到两个字符串和它们之间的对齐：

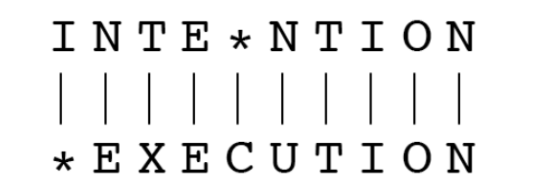
Performance：

  • Time：O(nm)
  • Space：O(nm)
  • Backtrace：O(n+m)

✎加权最短编辑距离

为什么要在计算中加权？

  • 拼写纠正：有些字母比其他字母更容易输入错
  • 生物学：某些类型的删除或插入更有可能发生

算法实现：

✎练习

动态规划实现求解最小编辑距离。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
def minEditDistance(word1, word2):
	m = len(word1) + 1
	n = len(word2) + 1
	dp = [[0 for i in range(n)] for j in range(m)]

	for i in range(n):
		dp[0][i] = i
	for i in range(m):
		dp[i][0] = i
	for i in range(1, m):
		for j in range(1, n):
			if word1[i-1] == word2[j-1]:
				dp[i][j] = dp[i-1][j-1]
			else:
				dp[i][j] = min(dp[i][j-1]+1, dp[i-1][j]+1, dp[i-1][j-1]+2)

	return dp[m-1][n-1]


word1 = "intention"
word2 = "execution"
print(minEditDistance(word1, word2))
0%